
Zadanie Profesor Szu (pro)
Pomóż nam usprawnić bazę zadań!
Profesor Szu
Limit pamięci: 32 MB
W mieście Bajtion ma swoją siedzibę bajtocki uniwersytet. Oprócz głównego
gmachu, uniwersytet ma do dyspozycji  domków dla pracowników naukowych.
Domki połączone są jednokierunkowymi drogami, może jednak być wiele dróg
łączących dwa domki, istnieją także drogi łączące gmach uniwersytetu z
domkami (droga może łączyć także pewien obiekt z nim samym).
Bajtion został tak skonstruowany, żeby żadne drogi się
nie przecinały w miejscach innych niż domki lub gmach (ale mogą przebiegać
mostami i tunelami); ponadto każda droga
zaczyna się w pewnym domku lub w gmachu i kończy się w domku lub
w gmachu. Wiadomo ponadto, że istnieje co najmniej jedna droga łącząca
pewien domek z gmachem uniwersytetu.
domków dla pracowników naukowych.
Domki połączone są jednokierunkowymi drogami, może jednak być wiele dróg
łączących dwa domki, istnieją także drogi łączące gmach uniwersytetu z
domkami (droga może łączyć także pewien obiekt z nim samym).
Bajtion został tak skonstruowany, żeby żadne drogi się
nie przecinały w miejscach innych niż domki lub gmach (ale mogą przebiegać
mostami i tunelami); ponadto każda droga
zaczyna się w pewnym domku lub w gmachu i kończy się w domku lub
w gmachu. Wiadomo ponadto, że istnieje co najmniej jedna droga łącząca
pewien domek z gmachem uniwersytetu.
Pewnego razu uniwersytet zapragnął zatrudnić u siebie znanego specjalistę informatyki teoretycznej - profesora Szu. Jak wielu wielkich naukowców, profesor Szu ma dziwny zwyczaj; otóż każdego dnia lubi dojeżdżać do gmachu uniwersytetu inną trasą (będącą drogą bądź układem dróg, z których każda następna zaczyna się w domku, w którym kończy się poprzednia; trasa może przechodzić przez ten sam domek bądź główny gmach uniwersytetu wielokrotnie). Profesor dwie trasy uważa za różne, jeżeli różnią się chociaż jedną wykorzystaną drogą (przy czym kolejność dróg jest ważna, a dwie różne drogi łączące te same domki uważa on za różne).
Znając schemat połączeń między domkami Bajtionu, pomóż uniwersytetowi
znaleźć domek, z którego istnieje najwięcej różnych tras do gmachu
uniwersytetu (zamieszkawszy w tym domku, profesor Szu będzie chciał
najdłużej pracować na uczelni) - jeżeli takich domków jest więcej niż
jeden, to podaj wszystkie z nich. Jeżeli przy tym z jakiegoś domku istnieje
więcej niż 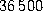 tras do gmachu, to zakładamy, że profesor może tam
zamieszkać na zawsze (jako że nie może żyć nieskończenie długo, a
tras do gmachu, to zakładamy, że profesor może tam
zamieszkać na zawsze (jako że nie może żyć nieskończenie długo, a 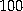 lat to dość bezpieczna granica).
lat to dość bezpieczna granica).
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia schemat połączeń między domkami Bajtionu,
- wyznaczy domki, w których profesor Szu mógłby mieszkać najdłużej oraz najdłuższy czas jego zamieszkiwania,
- wypisze wynik na standardowe wyjście.
Wejście
Pierwszy wiersz wejścia zawiera dwie liczby całkowite  oraz
oraz 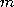 (
( )
oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę domków
i liczbę dróg w Bajtionie (domki są ponumerowane liczbami od
)
oddzielone pojedynczym odstępem i oznaczające odpowiednio liczbę domków
i liczbę dróg w Bajtionie (domki są ponumerowane liczbami od 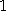 do
do  ,
a umownie nadajemy gmachowi uniwersytetu numer
,
a umownie nadajemy gmachowi uniwersytetu numer 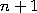 ).
W wierszach o numerach od
).
W wierszach o numerach od 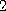 do
do  znajdują się pary liczb
całkowitych
znajdują się pary liczb
całkowitych 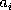 ,
, 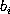 (
(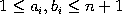 dla
dla  )
oddzielone pojedynczymi odstępami i oznaczające odpowiednio numer
domku w którym zaczyna się i numer domku w którym kończy się
)
oddzielone pojedynczymi odstępami i oznaczające odpowiednio numer
domku w którym zaczyna się i numer domku w którym kończy się  -ta
droga.
-ta
droga.
Wyjście
Pierwszy wiersz wyjścia powinien zawierać maksymalną liczbę dni jaką
profesor Szu może mieszkać w Bajtionie lub jedno słowo "zawsze", jeżeli
ta liczba przekracza 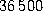 dni. W drugim wierszu powinna się
znajdować liczba domków, zamieszkanie w których zapewnia profesorowi
okres pobytu podany w pierwszym wierszu wyjścia. W trzecim wierszu
powinny się znaleźć numery wszystkich takich domków, oddzielone
pojedynczymi odstępami i podane w kolejności rosnącej. Wszystkie domki,
w których profesor może zamieszkać na zawsze uważamy przy tym za jednakowo
dobre.
dni. W drugim wierszu powinna się
znajdować liczba domków, zamieszkanie w których zapewnia profesorowi
okres pobytu podany w pierwszym wierszu wyjścia. W trzecim wierszu
powinny się znaleźć numery wszystkich takich domków, oddzielone
pojedynczymi odstępami i podane w kolejności rosnącej. Wszystkie domki,
w których profesor może zamieszkać na zawsze uważamy przy tym za jednakowo
dobre.
Przykład
Dla danych wejściowych:
3 5 1 2 1 3 2 3 3 4 3 4
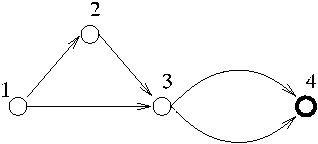
poprawnym wynikiem jest:
4 1 1
Natomiast dla danych:
3 5 1 2 2 3 3 1 3 4 3 4
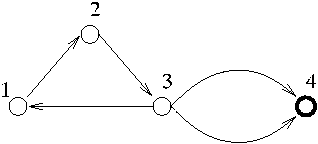
poprawnym wynikiem jest:
zawsze 3 1 2 3
Autor zadania: Jakub Radoszewski.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English